实小社团练习赛19

本文总阅读量次

8089,8729,8605,8732

T1

方法1：排序+去重扫描
排序后，线性扫描，相邻不同的时候，奖品种类+1。
方法2：map计数
答案为 $s i z e ()$

T2

枚举
虽然 $N$ 最大为 $10^{4}$ ，因为枚举区间是组合方式枚举，实际上时间复杂度为 $O (N^{2}) = 9999 + 9998 + . . . + 1 \approx 5 * 10^{7}$
所以，大胆枚举不会超时。

  for 枚举起点
      区间擂主初始化（找最小)
      for 枚举终点{
           打擂台找最小;
           计算当前区间能吃的橙子数
           橙子数量再打擂台
      }

注意枚举范围，一个盘子也要考虑。
这题只要会计算次数，就不会被难倒。
T3
排序+找规律
因为求的是绝对值，所以先把数
每个数即作为被减数，也作为减数，那么就会产生抵消，只要找出规律，快速计算出一个数被减数次数和减数次数，可以在 $O (N)$ 内解决。
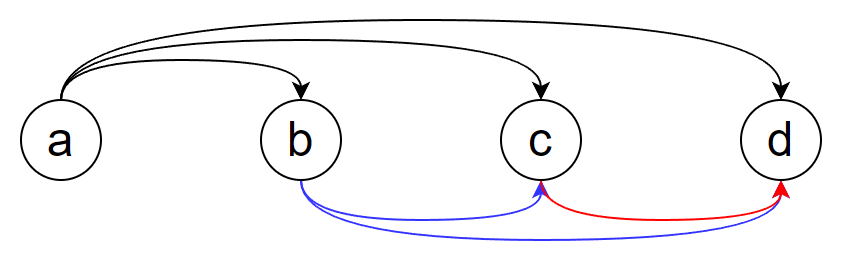
image.png|400

以上图为例：

数	被减数次数	减数次数
a	3	0
b	2	1
c	1	2
d	0	3
那么一个数贡献值为：(被减数次数-减数次数)×这个数
观察上表，也能发现被减数的次数规律为： $n - 1$ 、 $n - 2$ 、...、 $0$ ，结合 $i$ ，其实被减数次数为 $n - i$ 。
而减数的次数显而易见为 $i - 1$ 。
所以对 $a [i]$ 而言，贡献值为 $a n s + = (n - i - i + 1) * a [i]$ ，合并同类项后为 $a n s + = (n - 2 * i + 1) * a [i]$
可以验证，如果不排序，结果会错。所以先对数组进行排序。
最后输出别忘记加绝对值函数。

T4

DFS
显然把所有的情况都搜一遍，就能找到最优解。
但这题 $K$ 最大有16，如果采用组合方式搜索，时间复杂度为 $O (N!)$ ，即第一次 $D F S$ 搜索范围为 $N$ ,第二次为 $N - 1$ ，第三次为 $N - 2$ ...以此类推。 $16! = 20922789888000$ ，必然会超时，但能得到一部分分数。
组合式深搜:搜索写法，v数组表示盘子上有没有放碗

for(int i = x; i <= k; i++){
				if(v[c[i]] && v[d[i]]) dfs(i+1);
				if(v[c[i]]==0){
					v[c[i]] = 1;
					dfs(i+1);
					v[c[i]] = 0;
				}
				if(v[d[i]]==0){
					v[d[i]] = 1;
					dfs(i+1);
					v[d[i]] = 0;
				}
			}

正解做法
对第 $i$ 个人而言，他有两种放法，所以不从物品个数范围搜索，而从本身状态搜索，也就3个状态，要么放盘子 $C_{i}$ ，要么放盘子 $D_{i}$ ，要么不放。 $3^{16} = 43046721$ ，显然不会超时。
根据上面的分析，自己想一下如何去写深搜函数。