2024年8月赛丙组
本文总阅读量次
T1
模拟
答对加
#include<bits/stdc++.h>
using namespace std;
string s;
int ans;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>s;
for(int i = 0; i < s.size();i++){
if(s[i]=='Y') ans++;
else if(ans) ans--; //非0,可以扣分
}
cout<<ans;
return 0;
}
T2
数论
题意:告诉你首项、公差、项数,问有多少个素数。
显然要对等差数列中的每一项进行判断是否为素数。
两种思路:
- 生成等差数列,因为最多
个数,直接逐个判断是否为素数也能过。考虑极端情况,当 , , ,最后一项为 ,极限测试次数(假设每一项都是素数),大约 万次,所以不会超时。 - 筛法,数组不能开
,要开 ,否则会爆。
方法1:枚举方法判断
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,a,d,ans;
bool ss(int x)
{
if(x < 2) return 0;
for(int i = 2; i <= sqrt(x); i++){
if(x % i == 0) return 0;
}
return 1;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>a>>d;
for(int i = 1; i <= n; i++){
if(i == 1){ //首项
if(ss(a)) ans++;
}else{
a = a + d;
if(ss(a)) ans++;
}
}
cout<<ans;
return 0;
}
方法2:筛法判断,时间复杂度O(nlog(logn))
#include<bits/stdc++.h>
using namespace std;
const int N = 1e7+5;
int n,a,d,ans;
bool v[N];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>a>>d;
int MaxN = a+(n-1)*d; //计算出最后一项
v[1] = 1;
for(int i = 2; i<=sqrt(MaxN); i++){
if(v[i]) continue;
for(int j = 2 * i; j <= MaxN; j += i) v[j] = 1;
}
for(int i = a; i <= MaxN; i += d) //遍历等差数列
if(!v[i]) ans++;
cout<<ans;
return 0;
}
T3
数论
如果理解什么是互质数,这题就很简单。
互质数指的是两个数只有公因数
#include<bits/stdc++.h>
using namespace std;
int n,ans,a[100005];
int gcd(int x, int y)
{
while(x % y){
int r = x % y;
x = y;
y = r;
}
return y;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i = 1; i <= n; i++) cin>>a[i];
for(int i = 1; i < n; i++){
int t = gcd(a[i],a[i+1]);
if(t != 1) ans++;
}
cout<<ans;
return 0;
}
T4
数学规律
如果直接暴力枚举模拟,能拿
60分做法
for(int i = 1; i <= n; i++){
ans += n/i;
}
以
| n | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| n/i | 10 | 5 | 3.3 | 2.5 | 2 | 1.6 | 1.4 | 1.25 | 1.1 | 1 |
题目要的是商的整数部分,观察上面的表格,
以最后一个区间为例(商都是
不妨设商的整数部分为
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,sum;
int main() {
cin >> n;
for (int i = 1; i <= n; ) {
int val = n / i; //计算商的整数部分
int next_i = n / val + 1; //计算下一个区间的左端点位置
sum += val * (next_i - i); //快速求和
i = next_i; //i移动到下一个区间的左端点位置
}
cout << sum << endl;
return 0;
}
T5
贪心+数学
- “请你将其划分成
个连续段,并最大化每个连续段中最大值的和
满足这两个条件,会想到贪心。
最大化每个连续段中最大值的和不就是把前大的数相加吗?如果不是把前 大的数相加,那么和肯定不是最大。
所以,题目的第一个要求,其实就是把前大相加。
方案数如何计算?因为是个连续段,不妨画图分析,选取其中 个数分析。
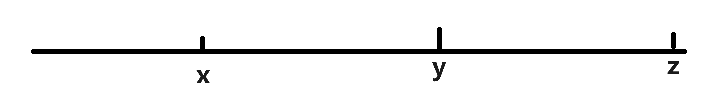
包含的区间个数有: 的位置- 的位置
画一下包含的区间如下:
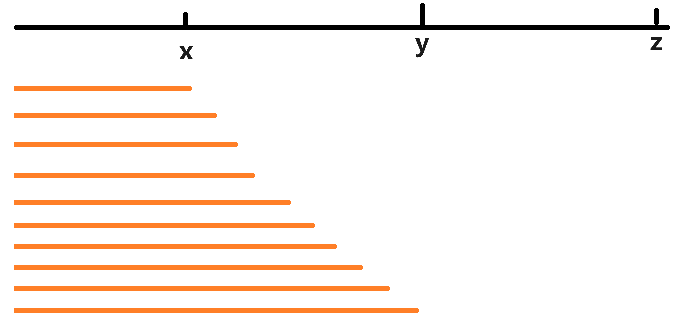
同理,包含的区间个数有: 的位置- 的位置。
所以方案数就是前大的数,包含这些数的区间个数相乘就是答案(乘法原理)。
具体做法,先按数从大到小排序,再把前个数按输入顺序从小到大排序(还原到原位置),然后计算出包含这些数的区间个数,用乘法原理进行计算。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
struct node{
ll v,p; //v表示给出的序列,p表示该数的位置
}a[100005];
bool cmp1(node x, node y) //根据v从大到小
{
if(x.v>y.v) return 1;
else if(x.v==y.v && x.p<y.p) return 1;
else return 0;
}
bool cmp2(node x, node y) //根据位置从小到大
{
return x.p<y.p;
}
ll n,m,ans = 0,cnt = 1;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i = 1; i <= n; i++){
cin>>a[i].v;
a[i].p = i;
}
sort(a+1,a+1+n,cmp1); //根据v从大到小排序
sort(a+1,a+1+m,cmp2); //根据输入位置从小到大排序
ans = a[1].v;
for(int i = 1; i < m; i++){
ans += a[i+1].v; //第一问:把m个数累加
ll dis = a[i+1].p - a[i].p; //计算区间个数
cnt = (cnt * dis) % mod; //乘法原理计算
}
cout<<ans<<endl;
cout<<cnt<<endl;
return 0;
}