2024年5月赛丙组
T1:加法的进位
模拟
数位对齐,模拟加法计算,统计进位次数。
注意数据规模,不需要字符串,整数模拟处理即可。
#include<bits/stdc++.h>
using namespace std;
int a,b,g1,g2,x,ans; //x保存进位的值
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>a>>b;
while(a>0||b>0){
g1 = a % 10;
g2 = b % 10;
if(g1+g2+x>9) ans++; //记得加之前的进位的值
x = (g1+g2+x)/10; //计算出进位的值
a/=10;
b/=10;
}
cout<<ans<<endl;
return 0;
}
T2:流水账
递推
题意要还原一开始小爱拥有的钱,所以可以采用倒推的方式来计算:支出改为“收入”,收入改为“支出”。
需要注意一个条件:小爱在任何时候拥有的现金额不会成为负数,所以一旦负数,需要清
#include<bits/stdc++.h>
using namespace std;
int n,a[100005],ans;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i = 1; i <= n; i++)
cin>>a[i];
for(int i = n; i > 0; i--){ //倒推
if(a[i]<0) ans += -a[i]; //支出还原为收入:负负得正,或者用abs()
else if(ans-a[i]>0) ans -= a[i]; //收入还原为支出
else ans = 0; //不够支出,则清0,满足题目的限制
}
cout<<ans<<endl;
return 0;
}
T3:发牌
队列
学过队列很简单,直接模拟即可。数组模拟也可以,但数组要开的大一些,大约50万不到。
#include<bits/stdc++.h>
using namespace std;
queue<int> q;
int n;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i = 1; i <= n; i++) q.push(i);
while(q.size())
{
int x = q.front();
q.push(x); //磨牌
q.pop();
x = q.front();
cout<<x<<"\n"; //发牌
q.pop();
}
return 0;
}
T4:距离之和
排序+数学
如果按题意两两枚举,则能拿
...
for(int i = 1; i < n; i++)
for(int j = i + 1; j <= n; j++){
ans += abs(x[i] - x[j]) + abs(y[i] - y[j]);
}
...
直接暴力会超时,所以不能按题意描述的去做。我们可以把
假设
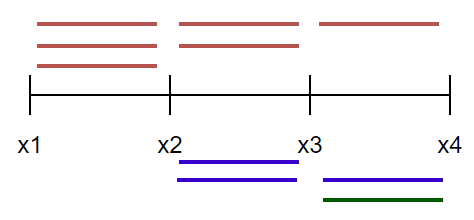
为起点,跟后面 个点组合一次, 会经过 次, 会经过 次, 会经过 次。 为起点,跟后面 个点组合一次, 会经过 次, 会经过 次。 为起点,跟后面 个点组合一次, 会经过 次。
假设
那么任意两点的距离之和为:
这样表达是为了把规律解释清楚,在
那么
那么当
这样计算距离总和的时间复杂度为
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MXN = 3e5+5;
LL n,x[MXN],y[MXN],dx[MXN],dy[MXN],ans;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i = 1; i <= n; i++){
cin>>x[i]>>y[i];
}
sort(x+1,x+1+n);
sort(y+1,y+1+n);
for(int i = 1; i < n; i++){ //计算相邻两个横坐标和纵坐标之间的距离
dx[i] = x[i+1]-x[i];
dy[i] = y[i+1]-y[i];
}
for(int i = 1; i < n; i++){
ans += dx[i]*(n-i)*i;
ans += dy[i]*(n-i)*i;
}
cout<<ans<<endl;
return 0;
}
T5:棋盘问题(二)
组合数学+高精度
毒瘤题×3!只考数学的话也还行吧,看到
题意:在棋盘上放置黑白两个不同的皇后,有多少种放置方法能够使两个皇后之间互相不能攻击对方。
如果情况很多,不好分析,我们可以逆向思考:两个皇后互相攻击有多少种放置方法。
- 两皇后在同一行上
- 两皇后在同一列上
- 两皇后在同一条斜线上
然后两皇后所有的排列情况-两个皇后互相攻击的种数=两皇后不能互相攻击的种数
下面分情况考虑。
两皇后在同一行上
方案数为:
两皇后在同一列上
方案数为:
两皇后在斜线上(先考虑一个方向)

假设
观察上图,斜线为
那么这几条斜线的方案数为:
观察上半部分的斜线,计算方案数:
也就是当
可以用平方和公式直接计算平方和:
把下半部分的斜线也算进去:
所以,这个方向的斜线的所有方案数为(中间长度为
再考虑另一个方向,方案数为:
最终,两个皇后互相攻击的方案数为:
两个皇后的所有排列方案为:
最终两个皇后互不攻击的方案数
因为是高精度,所以要实现高精度加、高精度减、高精度乘和高精度除以整数,实在太酸爽了。
为了方便处理返回的值,使用了
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;
string n,m;
vector<int>dn(maxn),dm(maxn),ans(maxn),two(maxn),one(maxn),three(maxn);
vector<int> add(vector<int> a, vector<int> b) //高精度加
{
vector<int>c(maxn);
int x = 0;
for(int i = 0; i < 500; i++){
x = a[i] + b[i] + x;
c[i] = x % 10;
x /= 10;
}
return c;
}
vector<int> sub(vector<int> a, vector<int> b) //高精度减
{
vector<int> c(maxn);
for(int i = 0; i < 500; i++){
if(a[i]<b[i]){
a[i] += 10;
a[i+1]--;
}
c[i] = a[i] - b[i];
}
return c;
}
vector<int> mult(vector<int>a, vector<int>b) //高精度乘
{
vector<int> c(maxn);
for(int i = 0; i < 500; i++){
int x = 0,j;
for(j = 0; j < 500; j++){
c[i + j] += a[i] * b[j] + x;
x = c[i + j] / 10;
c[i + j] %= 10;
}
}
return c;
}
vector<int> div(vector<int>a, int b) //高精度除以整数
{
vector<int> c(maxn);
int len = 0;
for(int i = a.size()-1; i >= 0; i--){
if(a[i]){
len = i;
break;
}
}
reverse(a.begin(),a.begin()+len+1); //先翻转
int x = 0;
for(int i = 0; i <= len; i++){
c[i] = (x * 10 + a[i]) / b;
x = (x * 10 + a[i]) % b;
}
reverse(c.begin(),c.begin()+len+1); //结果再翻转
return c;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
if(n.size()<m.size()||n.size()==m.size()&&n<m){
swap(n,m);
}
for(int i = n.size()-1; i >= 0; i--) dn[n.size()-i-1]=n[i]-'0';
for(int i = m.size()-1; i >= 0; i--) dm[m.size()-i-1]=m[i]-'0';
two[0] = 2;
one[0] = 1;
three[0] = 3;
vector<int> total = mult(mult(dn,dm),sub(mult(dn,dm),one));
ans =sub(total,add(mult(mult(dn,dm),sub(add(dn,dm),two)),div(mult(mult(mult(dm,sub(dm,one)),two),sub(mult(dn,three),add(dm,one))),3))); //公式转换,呵呵呵呵
int i = ans.size() - 1;
while(i>0 && ans[i]==0) i--;
for(; i >= 0; i--) cout<<ans[i];
return 0;
}
来见识一下
a = input().split()
n = int(a[0])
m = int(a[1])
if n<m:
n,m=m,n
print(n*m*(n*m-1)-(n*m*(n+m-2)+2*m*(m-1)*(3*n-m-1)//3))
所以,加减乘除的高精度轮一遍有意义么?